Dbscan
Density-based spatial clustering of applications with noise (DBSCAN) is a data clustering algorithm proposed by Martin Ester, Hans-Peter Kriegel, Jörg Sander and Xiaowei Xu in 1996. It is a density-based clustering algorithm: given a set of points in some space, it groups together points that are closely packed together (points with many nearby neighbors), marking as outliers points that lie alone in low-density regions (whose nearest neighbors are too far away). DBSCAN is one of the most common clustering algorithms and also most cited in scientific literature.
Preliminary
Consider a set of points in some space to be clustered. For the purpose of DBSCAN clustering, the points are classified as core points, (density-)reachable points and outliers, as follows:
- A point
pis a core point if at least minPts points are within distance ε (ε is the maximum radius of the neighborhood from p) of it (including p). Those points are said to be directly reachable from p. - A point q is directly reachable from
pif point q is within distance ε from pointpandpmust be a core point. - A point q is reachable from
pif there is a pathp1,...,pnwithp1 = pandpn = q, where eachpi+1is directly reachable from pi (all the points on the path must be core points, with the possible exception of q). - All points not reachable from any other point are outliers.
Now if p is a core point, then it forms a cluster together with all points (core or non-core) that are reachable from it. Each cluster contains at least one core point; non-core points can be part of a cluster, but they form its "edge", since they cannot be used to reach more points.
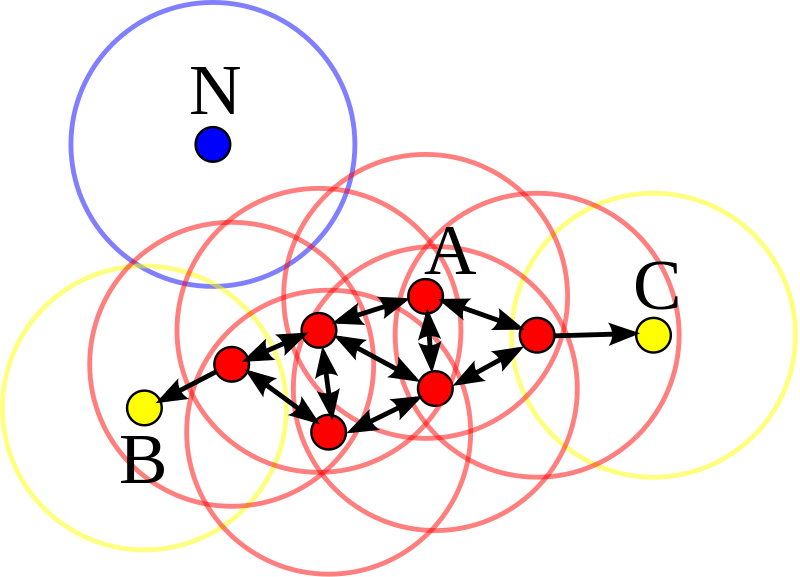
Reachability is not a symmetric relation since, by definition, no point may be reachable from a non-core point, regardless of distance (so a non-core point may be reachable, but nothing can be reached from it). Therefore, a further notion of connectedness is needed to formally define the extent of the clusters found by DBSCAN. Two points p and q are density-connected if there is a point o such that both p and q are reachable from o. Density-connectedness is symmetric.
A cluster then satisfies two properties:
- All points within the cluster are mutually density-connected.
- If a point is density-reachable from any point of the cluster, it is part of the cluster as well.
Algorithm
DBSCAN requires two parameters: ε (eps) and the minimum number of points required to form a dense region (minPts). It starts with an arbitrary starting point that has not been visited. This point's ε-neighborhood is retrieved, and if it contains sufficiently many points, a cluster is started. Otherwise, the point is labeled as noise. Note that this point might later be found in a sufficiently sized ε-environment of a different point and hence be made part of a cluster.
If a point is found to be a dense part of a cluster, its ε-neighborhood is also part of that cluster. Hence, all points that are found within the ε-neighborhood are added, as is their own ε-neighborhood when they are also dense. This process continues until the density-connected cluster is completely found. Then, a new unvisited point is retrieved and processed, leading to the discovery of a further cluster or noise.
DBSCAN can be used with any distance function (as well as similarity functions or other predicates). The distance function (dist) can therefore be seen as an additional parameter.
The algorithm can be expressed in pseudocode as follows:
DBSCAN(DB, distFunc, eps, minPts) {
C = 0 /* Cluster counter */
for each point P in database DB {
if label(P) ≠ undefined then continue /* Previously processed in inner loop */
Neighbors N = RangeQuery(DB, distFunc, P, eps) /* Find neighbors */
if |N| < minPts then { /* Density check */
label(P) = Noise /* Label as Noise */
continue
}
C = C + 1 /* next cluster label */
label(P) = C /* Label initial point */
Seed set S = N \ {P} /* Neighbors to expand */
for each point Q in S { /* Process every seed point */
if label(Q) = Noise then label(Q) = C /* Change Noise to border point */
if label(Q) ≠ undefined then continue /* Previously processed */
label(Q) = C /* Label neighbor */
Neighbors N = RangeQuery(DB, distFunc, Q, eps) /* Find neighbors */
if |N| ≥ minPts then { /* Density check */
S = S ∪ N /* Add new neighbors to seed set */
}
}
}
}
where RangeQuery can be implemented using a database index for better performance, or using a slow linear scan:
RangeQuery(DB, distFunc, Q, eps) {
Neighbors = empty list
for each point P in database DB { /* Scan all points in the database */
if distFunc(Q, P) ≤ eps then { /* Compute distance and check epsilon */
Neighbors = Neighbors ∪ {P} /* Add to result */
}
}
return Neighbors
}
Complexity
DBSCAN visits each point of the database, possibly multiple times (e.g., as candidates to different clusters). For practical considerations, however, the time complexity is mostly governed by the number of regionQuery invocations. DBSCAN executes exactly one such query for each point, and if an indexing structure is used that executes a neighborhood query in O(log n), an overall average runtime complexity of O(n log n) is obtained (if parameter ε is chosen in a meaningful way, i.e. such that on average only O(log n) points are returned). Without the use of an accelerating index structure, or on degenerated data (e.g. all points within a distance less than ε), the worst case run time complexity remains O(n²). The distance matrix of size (n²-n)/2 can be materialized to avoid distance recomputations, but this needs O(n²) memory, whereas a non-matrix based implementation of DBSCAN only needs O(n) memory.

DBSCAN can find non-linearly separable clusters. This dataset cannot be adequately clustered with k-means or Gaussian Mixture EM clustering
Implementation
| Language | Link | |
|---|---|---|
 | Python | dbscan.py |
